|
Is the Mean Better?
One or Two Measurements?
To increase accuracy you must try to make measurements
unbiased. You must also try to reduce variability. In the rifle
shooting Ann's shots were less varied than Barry's. In
measurement you want less variability. One way is to use the
mean. This section shows why using the mean reduces variability.
However, the mean is of no use if your results are biased.
Diana is measuring lengths. Equally often she is 1 mm under, 1
mm over and exactly right. This is illustrated in Figure 5.
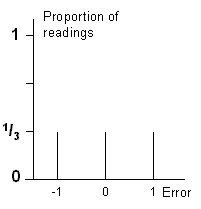
Figure 5 - Errors with one measurement.
| a |
Are Diana's measurements biased
or unbiased? |
Diana decides to take pairs of measurements and find the mean.
There are nine different outcomes, shown in Table 1. e.g. a
first measurement with error -1, followed by, a second
measurement with error -1, gives a total error of -2, which is a
mean error of -1.
| |
Second
Measurement |
| -1 |
0 |
1 |
| First
Measurement |
-1 |
-2 |
-1 |
0 |
| 0 |
-1 |
0 |
1 |
| 1 |
0 |
1 |
2 |
Table 1 - Total error in two measurements.
Table 2 on page R1 shows the mean error for some of these
figures.
From Table 2 you can see that one out of the nine outcomes
gives a mean error of -1. As a proportion this is 1/9
Two out of the nine outcomes give a mean error of -1/2.
As a proportion this is 2/9.
| c |
Calculate the proportion of
times her mean error is 0. |
| d |
Complete Table 3 on page Rl. |
| e |
Plot the proportion of different
size errors as a line graph. |
| f |
Write a sentence describing how
taking the mean of two readings improves accuracy over
taking one reading. |
Taking Four Measurements
Suppose Diaina took the mean of four measurements. It is
difficult to work out proportions in the same way. We can see
what happens by, throwing cubes or dice.
You will need four cubes (or dice).
On each of the four cubes mark two faces -1, two faces 0 and
two faces +1. When you throw the cubes, the faces show the error
Diaina made so that -1, -1, 0, 1 gives a total error of -1, which
is a mean error of -1/4.
(If you have dice use the following code: one and two
become -1, three and four become 0, five
and six become + 1).
| a |
Throw the cubes. Add the numbers
to get the total error. Make a tally mark in Table 4 on
page R1. |
| b |
Repeat until you have 40 throws. |
| c |
Complete Table 4. |
| d |
Plot the proportion of different
size mean errors as a line graph. |
| e |
What proportion of your results
gave zero mean error? |
| f |
What proportion of your results
gave a mean error of -1 or +1? |
| g |
Write two sentences comparing
the mean errors of four measurements with the error when
only one measurement is taken. |
|