|
How Accurate?
Measuring
You will need a ruler, a protractor, tracing paper marked with
a square cm grid and a sheet of paper.
| a |
Find, as accurately as you can,
the distance in cm from one corner to the opposite corner
of the sheet of paper (the diagonal). |
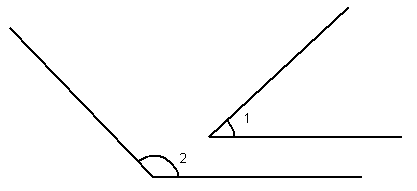
Figure 1 - Two angles
| a |
Measure angles 1 and 2 in Figure
1 as accurately as you can. Record your results. |
| b |
Find the area of Figure 2 in sq
cm It is a map of Lough Neagh in Northern Ireland. |
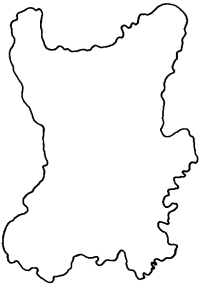
Figure 2 - Lough Neag
Some Results
| |
John |
Ann |
| Paper |
35 cm (to nearest 5 cm) |
35.831 cm (to nearest 1/1000 cm) |
| Angle 1 |
40o (to nearest 10o) |
43. 7o (to nearest 1/10o) |
| Angle 2 |
130o (to nearest 10o) |
46. 7o (to nearest 1/10o) |
| Region |
20 sq cm (to nearest 5 sq cm) |
18.21 sq cm (to nearest 1/100 sq
cm) |
| a |
John measured the paper to the
nearest 5 cm. Could you tell the difference between a
sheet 35 cm long and another 40 cm long?
Is it sensible to measure to the nearest 5 cm? |
| b |
Do you think John used his
protractor and squared paper as accurately as he could?
Why? Are his answers sensible? |
| c |
Ann measured the area of the
region to the nearest 1/100 sq cm.
Could you tell the difference between an area of 18.21 sq
cm and an area of 18.22 sq cm? Is it sensible to measure
to the nearest 1/100 sq cm? |
| d |
Do you think Arm used her ruler
to give a sensible answer? Why? |
| e |
In fact Ann obviously measured
angle 2 incorrectly. Explain what might have happened. |
Class Results
Twelve members of Class 2X got these results in measuring the
width of a sheet of paper in cm:
20.8, 20.8, 20-9, 20.7, 8.2, 20.6,
20.8. 20-8, 20.7, 20.8, 20.9, 20.7.
The answers are not all the same because different pupils have
measured the width. However, one result for Class 2X is obviously
wrong.
| a |
Write down this answer and try
to explain what might have happened. |
The other 11 results are nearly the same; but they are not
wrong.
| b |
Why do you think they differ?
How would you decide what answer to give? |
| c |
Copy and complete this sentence
with a sensible answer:
The width measured by Class 2X is about _____cm. |
| d |
Copy and complete this sentence
(ignoring the result 8.2 cm):
The results of Class 2X ranged from cm to cm. |
You will need votir class measurements from your teacher. Look
at each set of measurements, starting with the lengths.
| |
e |
Is any measurement a lot
different from the rest? If so, tell your teacher and try
to find out why. Cross it out of your results. |
| |
f |
Write down the lowest
measurement and the highest measurement. What is a
sensible answer for the measurement? |
| |
g |
Repeat c and f for your class
answers on the two angles. |
| |
h |
Repeat e and f for your class
answers on the area of the region. |
| * |
i |
Sometimes errors can arise from
faulty measuring instruments. Check your ruler with that
of a friend by placing the rulers edge to edge. Check
your protractor by measuring angles 1 and 2 with someone
eise's protractor. Write down what you find. |
The Mean
When results vary, we can use the arithmetic mean to get a
more accurate answer. Class 2X left out the 8.2cm (which was
wrong) and found the mean of their results.
(20.8 + 20.8 + 20.9 + 20.7 + 20.6 + 20.8 + 20.8 + 20.7 + 20.8
+ 20.9 + 20.7)cm / 11
= 20.77 cm (to two decimal places)
Notice that they gave their answer to two decimal places,
because taking the mean should give a slightly more accurate
answer.
| a |
Find the mean of your class
results on the length of the diagonal. |
| b |
Find the mean of your class
results on the two angles. |
| c |
Write down two sentences
describing your results. |
Estimating More Accurately
Finding the area of the lake in Section Bl was not easy
because you had to count part squares. You can get a
more accurate answer by repetition.
| a |
On tracing paper,draw a set of
dots at l cm intervals like this. Cover the whole sheet. |
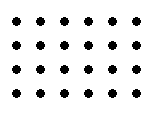
The dots are the centres of 1 cm squares.
| b |
Place your tracing paper to
cover the region in Figure 2 so that as few dots as
possible are inside. Write down the number of dots
inside.
Now place your tracing paper to cover the region so that
as many dots as possible are inside, and write
down that number.
Use these two numbers to give estimated limits to the
area of the region. |
| c |
Let your tracing paper fall to
cover the region. Write down the number of dots inside
the region. |
| d |
Repeat c until you have 10
results. Find the mean of your 10 results to estimate the
area of the region. |
| e |
Write a sentence describing your
results. |
In this section you have seen that when different people
measure the same thing they get different answers. You
may also get different answers when you measure the same thing
twice yourself. This is called human error.
One way to reduce human error and variability is to take
several results and find the mean. But you must
make sure that all the answers you use are sensible: if one
answer is obviously wrong, you should ignore it.
*Boxes
Sometimes you need to guess weights, perhaps in cooking or
when buying food. If you do not have scales, you can try
comparing weights.
In this experiment your teacher will give you seven boxes
(A,B,C,D,E,F,G) and a standard box (Z). Compare box A with box Z.
If box A is lighter than box Z, put a slip of paper marked l
in envelope A. If box A is heavier, use an h; if it is
the same, use s. Repeat for the other six boxes.
Your teacher will give you the class results.
| a |
Work out the 'score' for each
box, h - 1. Put the boxes in order, starting with the
lightest. The standard box has a score of 0. |
| b |
Compare your class results with
the true order which your teacher will give you. |
|