Target Shooting
Spotting Bias
Useful Bias
Summary
|

|
Bias
Target Shooting
Ann and Barry go to a fair together. They try their luck
shooting at a target. They each use the same rifle and get the
results shown in Figure 3. The cross ( x
) marks the bull's-eye.
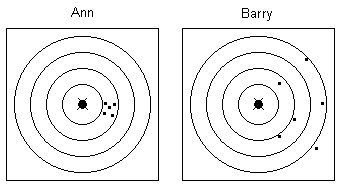
Figure 3 - First attempt
| a |
Write one sentence comparing
Ann's and Barry's results. |
| b |
No shots hit the left-hand side
of the target. Why do you think this might happen? |
| c |
Why do you think neither of them
hit the bull's-eye? |
Ann's shots are close together. They are to one side of the
target. Her aim is biased.
Barry's shots show greater variation. They are to one side of
the target. His aim is biased.
Ann and Barry look at their results. They decide to have
another go with the same rifle. But they agree to aim left of
centre. Figure 4 shows their results.
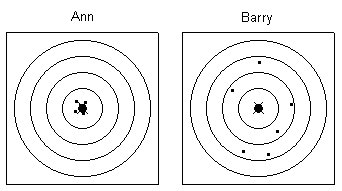
Figure 4 - Second attempt
| d |
Write two sentences to compare
their results this time. |
| e |
Have a look at your answer to b.
If you want to change it, write your new version now. |
Look at Ann's results. The first time all her shots were close
together on the right. The second time, with the same rifle she
aimed to the left and all her shots were close to the bull's-eye.
The rifle must have been BIASED to the right.
| f |
Are Barry's results better when
he aims to the left? |
On his second attempt, Barry's shots still vary widely. His
shots now balance round the centre. His aim is now unbiased. But
he is not accurate.
On her second attempt, Ann's shots still do not vary much.
They are also unbiased. Her shooting is accurate.

Spotting Bias
Sometimes a measuring instrument is biased. All its
measurements may be too low or too high. It is not always easy to
spot bias, except by checking with another instrument (which you
know is correct).
Below are some measurements made with different instruments.
You have to decide whether or not each instrument is biased.
Remember that the measurements will vary a little because of
human error; you are looking for bias. Look at the set of
readings for each instrument or example. In each case write only
one of the following:
biased above, unbiased or biased below
| a |
Water boils at 100'C.
| (i) |
Thermometer 1: 1OOoC,
100oC,
101oC,
99oC,
100oC |
| (ii) |
Thermometer 2: 97oC,
98oC,
95oC,
99oC,
90oC |
| (iii) |
Thermometer 3:104oC,
100oC,
107oC,
105oC,
103oC,
99oC |
| (iv) |
Thermometer 4: 98oC,
101oC,
100oC,
101oC,
100oC |
|
| b |
The diagonal of a 5 cm square is
7.1 cm.
| (i) |
Ruler 1: 7.0 cm, 7.2 cm, 7.2 cm, 7.1
cm, 7.1 cm |
| (ii) |
Ruler 2: 6.4 cm, 6.3 cm, 6.5 cm, 6.3
cm, 6.5 cm |
If the same ruler was used in both cases,
suggest what might have happened.
|
| c |
Colin uses his calculator to add
up some figures. |
| d |
A teacher measures the heights
of a class of girls when they are wearing shoes. |
| e |
Sarah weighs with a pair of
scales and then finds some plasticine underneath the
scale in which she puts weights. |
| f |
Give an example of a measurement
which is biased. |
| g |
Give an example of a measurement
which is unbiased. |
In science and elsewhere we usually want measurements which
are unbiased. Unbiased measurements can be either side of the
accurate answer; on average they will be correct.
Useful Bias
Sometimes it is useful to take biased measurements. We have
already seen that measurements can vary because of human or
instrument error. This variation could lead to a disaster. Read
the example below to see how bias can help.
An engineer estimates a bridge can carry a load of 190 tons.
Because of variation in manufacture, the bridge may only he able
to support 180 tons. If 19 ten-ton lorries cross together, the
bridge would collapse. To avoid this the engineer would give a biased
estimate of how much the bridge could carry, perhaps 150 tons. In
this way he can allow for variation. He knows the bridge will be
safe if the load is never more than 150 tons.
Look at the examples below. You need to think about what will
happen if you end up with a smaller or bigger amount than the
true value. In each case decide whether You would take more or
less than the true value.
| a |
A driver estimates his stopping
distance to be 120 feet. How far before a zebra crossing
should he start to brake? |
| b |
A woman wants to tile her
kitchen: the area is the same as the area of 242 square
tiles. How many tiles should she buy? |
| c |
A man wants to fix a window in a
frame. Should he buy a pane of glass which is slightly
bigger than the frame or slightly smaller? |
| d |
You want to save up over the
next eight weeks to buy a £4.00 record album. How much
should you save each week to avoid disappointment? |
| e |
A mother wants to wallpaper her
daughter's room. The area is the same as 2.5 rolls of
wallpaper. How many rolls of wallpaper should she buy? |
| f |
A girl is buying lace to put on
her dress. She finds she will need 163 cm. How much
should she buy? |
| g |
A motorist is travelling in a 50
mph speed limit area. How fast should he go if he is in a
hurry but does not want to be stopped by the police? |
| h |
A boy needs 6 oz of flour in a
cake mixture. Should he put in just less or just more
before testing the dropping consistency? |
Summary
To get accurate answers your measurements should be unbiased
and vary as little as possible.
When you are using measurements, you must make sure that your
final answer is sensible. Give your answer to about the same
number of significant figures as the measurements you started
with. If your readings are unbiased, using the mean improves
accuracy
|