|

Fruit Machines
A Simple Spinner
One class has decided to design and make a fruit machine.
They start with a regular hexagonal spinner. After being spun,
only one of the six triangular sectors shows.
They paint:
- Cherries on 3 sectors
- An orange on 2 sectors
- An apple on 1 sector
They call this Spinner I (Figure 7)
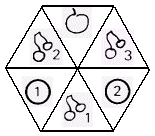
Figure 7 - Spinner I.
There are cherries on three out of six sectors.
The probability of getting cherries = 3/6
| a |
Copy and complete the following:
The probability of getting an orange is _____.
The probability of getting an apple is _____.
The probability of getting cherries is _____. |
| b |
Add these probabilities
together. Write down your answer. |
Alan suggests 'We could give a prize if they spin an orange or
an apple.' This suggestion is accepted.
| c |
On how many sectors can a player
win? |
| d |
What is the probability of
winning? |
Peter says:
'Probability of winning = Probability of an orange + Probability
of an apple.'
| e |
Put the correct figures in this
statement. Is Peter right? |
| f |
What is the probability of not
winning? |
| g |
Look at your answers to d and f
to copy and complete the following:
The probability of winning + The probability of not
winning = _____. |
Using Two Spinners
Shella suggests that the fruit machine ought to have two
spinners to make the game more interesting. Spinner II is made
(Figure 8).
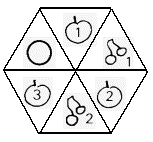
Figure 8 - Spinner II.
On Spinner II they paint:
- Cherries on 2 sectors
- An orange on 1 sector
- An apple on 3 sectors
A game consists of spinning both spinners once. NOTICE:
Spinner I has six sectors. Spinner II has six sectors. Any sector
on Spinner I could come up with any sector on Spinner II. So
there are 36 pairs of sectors.
The result on one spinner does not affect the result on the
other.
Table 3 shows the 36 pairs of possible results. Each one of
these is equally likely to come up.
| |
Spinner II |
| Spinner I |
|
 |
 |
 |
 |
 |
 |
 |
|
|
|
ca |
ca |
ca |
 |
|
|
|
ca |
ca |
ca |
 |
|
|
|
ca |
ca |
ca |
 |
|
|
|
|
|
|
 |
|
|
|
|
|
|
 |
|
|
|
|
|
|
Table 3 - Results on the two spinners.
The nine places which show cherries on Spinner I and an apple
on Spinner II are marked ca.
REMEMBER: Read Spinner I first, then Spinner II.
In Table 6 on page R1:
| a |
Mark the places which show
cherries on both spinners with ca. |
| b |
Complete the other squares in
the table with co, oc,
ac, oa,
ao, oo,
aa. |
The combination ca occurs on 9 out of 36 squares. The
probability of getting cherries on 1 with an apple
on 11 (ca) is 9/36 = 1/4.
| c |
What is the probability of
getting an apple on I with cherries on II (ac)? |
The probability of getting an orange on both spinners is 2/36.
The pobability of getting an apple on both spinners is 3/36.
The probability of getting oranges on both spinners or apples
on both spinners is: 2/36 + 3/36
= 5/36.
| d |
What is the probability of
getting:
cherries on both spinners,
apples on both spinners,
either cherries on both spinners or apples on both
spinners? |
| e |
What is the probability of
getting:
an orange on I and an apple on II,
an apple on I and an orange on II,
an apple and an orange in either order?
Use your Table 6 to find: |
| f |
The probability of getting two
of the same fruit. |
| g |
The probability of getting two
different fruits. |
Jane says: 'We should give a prize for getting the same fruit
on each spinner.'
| h |
What is the probability of
winning? |
How Much to Charge?
John says: 'We should give larger prizes to the winning lines
that are harder to get.' The class agrees to give:
- 5p for cherries on both spinners
- 10p for apples on both spinners
- 15p for oranges on both spinners
They want to know how much to charge for each game.
| a |
Copy and complete the following
to help them decide.
In 36 games we expect to get:
Cherries on both spinners six times.
This pays 6 x
5p = 30p.
Apples on both spinners _____ times.
This pays _____ = _____ p.
Oranges on both spinners _____ times.
This pays _____ = _____ p.
We expect to pay out _____ p in 36 games.
On average we expect to pay _____ p per game. |
| b |
How much should they charge per
game? |
| c |
How much profit would they
expect to make each game? |
| d |
How much profit would they
expect to make in 500 games? |
*More Fruit Machines
| a |
Design your own two spinners
with more sectors and extra fruits. Make up your own
rules for prizes and winning lines. |
| b |
Design a third spinner. Work out
the probabilities of winning by getting the same fruit on
all three spinners. You may need help from your teacher. |
|