|
Brief Description
Pupils are encouraged to design stalls for a summer fair. The
stalls are analysed probabilistically to help decide on entry
fees and prizes which will maximize profits.
Design Time: 4-5 hours.
Aims and Objectives
On completion of the unit pupils should be able to use
relative frequencies from experimental results and also to assign
and use probabilities from expected results in simple equally
likely cases. They will have practised both of these techniques
in the context of calculating expected profits (or losses). They
myet directly and intuitively the addition rule and complementary
rule of probabilities through simple examples of both. They
should be more aware of the fundamental problems of designing
profit-making stalls, dependent upon random variation and the use
of probability theory in modelling statistical situations.
Prerequisites
Addition of simple fractions.
Simplification of fractions.
The use of negative numbers to indicate a loss.
It would help if pupils have some notion of assigning
probability in equally likely cases (simple coin tossing or
rolling 1 die).
Equipment and Planning
Sheets of centimetre square graph paper, a number of pennies
and a large 4 cm by 4 cm diagonal square grid are required for
Section C. (More large sheets are needed if pupils work
in pairs or groups.) A model, large scale or to size, is needed
of one 4 cm by 4 cm square to show the area in which the centre
of a 1p coin must lie in order that the coin lies completely
inside the square. It is suggested that with the model a card
replica of a 1p coin is used with a hole in the centre through
which a pencil may be put, so that the area in which the centre
of the coin must lie can actually be shaded in.
Section *C3 is optional and is designed for less able
pupils to help them see more clearly the argument for theoretical
probabilities in the game of push penny (Section C4).
Similarly, Sections C6, D4 and E4 are
optional sections designed for faster and more able pupils.
Sections B, C, D and E can be
attempted in any order, though E is the hardest. It is
possible to arrange the Sections B, C and D
as a 'circus', in which groups of children try each section in
turn.
Detailed Notes
Section A
This introduction could well be used for a discussion of the
important aspects of designing stalls for a summer fair. Quite
often the entry fee and prizes are decided arbitrarily,
occasionally yielding a loss over the whole day, to the chagrin
of the organizers. All the stalls analysed are assumed to involve
no skill, though there are some questions considering this
possibility.
Naturally the main purpose of the fair is to make money,
though it is also important that people should enjoy themselves.
Each stall should make money. However, if the expected profit,
and therefore loss to players, is too high, few people will take
part, so that little money will be made. If the expected profit
is too low, again little money will be made. To attract people it
is often useful to have a high prize with a low chance of winning
it and a large number of small prizes (less than the entry fee)
to encourage people to participate. These points are brought out
through examples, but there is scope for extension if pupils do
get involved: a raffle, darts (though here skill is involved),
rolling balls, roulette wheels, bingo, etc.
Section B
B1
The stallholder's profit per game is determined by the
size of the entry fee alone, and the only consideration is how
large a fee can be charged so that people will still play. ALL 10
TICKETS MUST BE SOLD BEFORE PLAYING THE GAME.
- Probably not, people would not buy tickets for £1.
B2
This section introduces the idea of using probability to
measure the likelihood of winning. The concepts of expected loss
and average loss, both important concepts, are introduced here
and again in later sections. The fact that expected loss need not
be an integer could be pointed out to more able pupils, through
the example of average family size being 2 adults and 2.4
children or by changing the value of the bear to £1.25. Less
able pupils may need help in understanding this idea when it
occurs in B2e.
- He is certain to lose 50p each time.
The parallels with bingo might be made at the end of this
section with a more able group. There is a guaranteed profit,
identical to B1 if 10 tickets are sold for 20p and a £1.50
prize given. The idea can be extended to the selling of more
tickets and multiple prizes.
Section C
The results can be collected as a class, or by groups or pairs
of pupils. Each group will require a large grid of squares 4 cm
by 4 cm, stuck flat on a table top and coins pushed as in shove-ha'penny.
The grid is diagonal to reduce the effect of skill through
pushing parallel to the lines. Working in pairs or groups is more
valuable to pupils in showing variation as well as providing data
for C2f. Other grids of different sizes could be
used for *C6. Another possibility is to have the grid
laid out as below, to investigate the effect of skill in pushing
the pennies on a line perpendicuhr to the edge.
The principle of using areas to work out probabilities can be
extended through darts' games, where darts are thrown at three
separate cards on a board or in aiming at the 1 on a £1 note.
C2
- The problem of variation with a small sample of 20 is
inevitable, and collecting data together from the whole
class should eliminate the freak results and give a
relative frequency of success near to the theoretical 1/4.
*C3
This look at the simpler board, as in the old game of
shove-ha'penny, is to lead in to the idea of using areas to
evaluate probabilities. The lines on the centimetre-square paper
can be used to emphasize the position of the centre of the penny
as it moves from losing to winning positions. The winning
positions can be demonstrated by putting rulers 4 cm apart and
moving the coin between them. The probability is 1/2
if we assume no skill, so that the centre of the coin is equally
likely to land on any point in the 4 cm between the two
successive grid lines.
An alternative to using the centre of the coin is to look at
the leading edge of the coin. As the penny moves from position A
to position B, the coin is in a winning position when
its leading edge is in the shaded region on the right. This
alternative, though, does give extra difficulties when extended
to the square grid in C4.
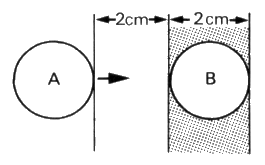
e-g In general if the grid lines are x
cm apart and the coin has diameter d cm, then the
probability of winning is x - d
/ x
C4
The winning position can be demonstrated by making a
square with raised cardboard edges; a circular disc with a hole
in the centre, putting a pencil through the hole and moving the
disc inside the square.
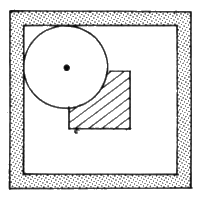
The probability of winning is 1/4, which
is 1/2 x 1/2 and is
an example of the product of two independent probabilities. Some
fairgrounds use thick lines around their squares. The effect of
this can be discussed with the class.
| e, f |
Clearly a prize of 2p is most
profitable to the stallholder; 3p makes a smaller
profit; 4p gives zero profit. Since Sp makes a loss
of 25p on average in 100 games, it would clearly not
be offered as a prize. |
C5
A player improves his chances the more tries he takes,
since skill plays a part, and the competitor learns techniques.
Pupils may suggest making smaller squares with larger prizes
and larger squares offering only money back. The effects on
probability of the size of the square is dealt with in C6.
*C6
For a grid with square sides x cm and a coin
diameter d, the probability of winning is 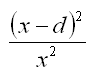 . .
| g, h |
The probabilities of winning are 1/9
and 4/9 so the expected number
of wins in 100 pushes is 111/9
and 444/9 respectively. Since
this is difficult to interpret, it may be advisable
to suggest working out the expected profit to the
stallholder in 99 throws. The answers then become: g
expected profit 99p 22p = 77p;
h expected profit 99p 88p = 11p.
|
The most common grid in use at school fairs, etc., uses
squares of different sizes and prizes relative to the difficulty
involved. Working out the probabilities and profits here is made
more complicated by the blank spaces that occur on the board.
Section D
From the stallholder's point of view this differs from Section
B in that the actual profit made in each game cannot be
predetermined. This time he, like the player, has to work with
expected profit. However, the stallholder can take results as
averaging out over a large number of games and can be fairly
certain of a profit. The player has to consider each game
individually.
The psychological advantage of everyone getting a prize
encourages people (especially young children) to play.
D3
Jane's suggestion brings out the point that it is
useless for the organizers to have a large number of players if
each game has an expected loss rather than profit.
D4
Gary's suggestion goes against the psychological
advantage of a prize every time.
Section E
Some pupils may find this section difficult and need help.
The fruit machine is used to establish and work with simple
assignment and addition of probabilities. These probabilities are
finally linked with expected profits.
The section could be approached practically, though
professionally made spinners would be necessary to avoid bias. A
spinner with three sectors on an equilateral triangle may help
less able pupils. Cocktail sticks make good axes.
The winning sector can be shown by drawing an arrow at the
side of the hexagon, putting a drawing-pin in the centre of the
hexagon and spinning the hexagon.
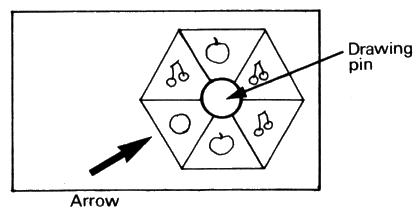
The underlying points of the section are:
- P(A or B) = P (A) + P(B),
if A and B are mutually exclusive
- P(not A) = 1 - P(A)
- If A has m outcomes and B has n
outcomes, then A followed by B has mn
outcomes.
E2
The fruit on the spinners has been numbered to help show
the 36 different combinations. Some pupils may find it helpful to
compare this with the table showing the 36 different combinations
on throwing two dice (say a red one and a blue one).
*E4
This is definitely only for the most able pupils.
- The third spinner gives 216 possible outcomes, and the
probabilities for winning can be obtained best from P(A
and B) = P(A) x P(B), if A
and B are independent. There are indications of
simpler applications of this rule in the table in E2.
Answers
| A |
|
See detailed notes. |
| |
|
|
| B1 |
a |
15p |
| |
b |
151/2 p (or 16p) |
| |
c |
See detailed notes. |
| |
d |
20p is a reasonable answer. |
| |
|
|
| B2 |
a |
£2.00 |
| |
b |
£1.50 |
| |
c |
50p |
| |
d |
Gary expects to lose 50p in 10 games.
This is an average of 5p each game. |
| |
e |
See detailed notes. |
| |
|
|
| C3 |
e |
1/3 |
| |
f |
3/5 |
| |
g |
4/6 or 2/3 |
| |
|
|
| C4 |
b |
100p - 75p = 25p |
| |
c |
100p - 100p = 0p |
| |
d |
100p - 125p = -25p, a loss |
| |
e and f |
See detailed notes. |
| |
|
|
| C5 |
|
See detailed notes. |
| |
|
|
| *C6 |
c |
25 cm2 |
| |
d |
9 cm2 |
| |
e |
9/25 |
| |
f |
100p - (2 x 36)p = 28p |
| |
g |
Outer area 9 cm2, inner area
1 cm2, probability 1/9,
expected profit 777/9p |
| |
h |
Outer area 36 cm2, inner area
16 cm2, probability 4/9,
expected profit 111/9p |
| |
i |
See detailed notes. |
| |
j |
See detailed notes. |
| |
|
|
| D1 |
a |
4 |
| |
b |
40p |
| |
c |
Missing values on table are 30p, 25p, 40p,
25p giving a total of £1.60. |
| |
d |
£1.60 |
| |
e |
4p |
| |
f |
Probably 5p (or 10p) |
| |
g |
1p if charge is 5p |
| |
|
|
| D2 |
a |
1p |
| |
b |
£8.00 |
| |
c |
3/4 |
| |
d |
3/4 |
| |
e |
3/4 |
| |
f |
1/40 |
| |
|
|
| D3 |
a |
Yes |
| |
b |
£2.10 |
| |
c |
51/4 |
| |
d |
Almost certainly not. A loss of £2.00
would be expected. See detailed notes. |
| |
|
|
| *D4 |
a |
2p |
| |
b |
3p |
| |
c |
See detailed notes. |
| |
|
|
| E1 |
a |
1/3, 1/6,
1/2 |
| |
b |
1 |
| |
c |
3 |
| |
d |
3/6 = 1/2 |
| |
e |
= 2/6 + 1/6.
Yes |
| |
f |
3/6 |
| |
g |
1 |
| |
|
|
| E2 |
c |
2/36 |
| |
d |
3/36, 3/36,
9/36, or 1/6,
1/12, 1/4 |
| |
e |
6/36, 1/36,
7/36 |
| |
f |
6/36 + 2/36
+ 3/36 = 11/36 |
| |
g |
1 - 11/36 = 25/36 |
| |
h |
11/36 |
| |
|
|
| E3 |
a |
Apples on both three times. This pays 30p.
Oranges on both two times. This pays 30p. 90p in 36 games:
21/2p per game. |
| |
b |
Probably 5p |
| |
c |
21/2p |
| |
d |
£12.50 from a charge of 5p |
Test Questions
- A fair has a horse race with 20 horses. Twenty people
each bet Sp on a different horse. The winner gets 50p.
- What is the probability of a particular person
winning?
- What is the profit to the fair on each race?
- In a game of bingo 100 cards are sold at 5p each. A prize
of £3.00 is given. What is the probability of winning if
you buy:
- 1 card
- 5 cards
- 10 cards
- In a game of push penny the stallholder keeps your penny
but pays a prize of 2p if you win. In 100 pushes 30 coins
land completely inside a square.
- How much money is taken?
- How much money is paid in prizes?
- What is the profit to the stall in these 100
pushes?
- On each wheel of a fruit machine with 12 sections there
are four cherries, three apples, three oranges and two
pears.
- What is the probability of getting a cherry?
- What is the probability of getting a pear?
- What is the probability of getting a cherry or a
pear?
- What is the probability of getting an apple?
- What is the probability of not getting an apple?
- On a die with no numbers one face is painted red, two are
painted blue and three painted green.
- What is the probability of rolling a green?
- What is the probability of not rolling a blue?
A game costs 10p and consists of rolling the die once.
If a red is thrown a prize of 20p is paid.
If a blue is thrown a prize of 12p is paid.
- Copy and complete the
following:
The stallholder says:
In six throws I expect to see a red _____ times
and pay _____ p.
In six throws I expect to see a blue _____ times
and pay _____ p.
In six throws the money taken = _____ p.
In six throws the prize money = _____ p.
In six throws the profit to the stall = _____ p.
- What profit does the stall expect to
make on average in 1 throw?
- A red disc 2 cm in diameter has a 1 on one side and a 2
on the other. A similar blue disc has a 2 on one side and
a 3 on the other. A game consists of tossing both discs
together and writing down the red number and then the
blue number to give a two-figure number such as 12, 23.
- What is the smallest number you can make?
- How many ways can you make this score?
- What is the largest number you can make?
- How many ways can you make 22?
- How many possible numbers can you make?
The game is won by scoring 22.
- What is the probability of winning?
The game costs 5p. The stallholder always keeps this.
If you win he gives you 15p. You play 20 games.
- In how many games do you expect to win?
- How much will 20 games cost?
- How much will you expect to win in prizes?
- What is the stallholder's expected profit in 20
games?
- A red die and a blue die are thrown and the numbers added
together. Copy and complete the table to show the
possible results.
| |
Red die |
| 1 |
2 |
3 |
4 |
5 |
6 |
| Blue die |
1 |
|
|
4 |
|
|
|
| 2 |
|
|
|
|
|
|
| 3 |
|
|
|
7 |
|
|
| 4 |
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
- In how many ways can you score a total of five?
- How many different ways can the two dice fall?
- What is the probability of scoring a total of
five?
- What is the probability of scoring a total of
seven?
- What is the probability of getting a double six?
- What is the probability of getting any double?
Answers
| 1 |
a |
1/20 |
| |
b |
50p |
| |
|
|
| 2 |
a |
1/100 |
| |
b |
5/100 = 1/20 |
| |
c |
10/100 = 1/10 |
| |
|
|
| 3 |
a |
£1.00 |
| |
b |
60p |
| |
c |
40p |
| |
|
|
| 4 |
a |
4/12 = 1/3 |
| |
b |
2/12 = 1/6 |
| |
c |
4/12 + 2/12
= 6/12 = 1/2 |
| |
d |
3/12 = 1/4 |
| |
e |
9/12 = 3/4 |
| |
|
|
| 5 |
a |
3/6 = 1/2 |
| |
b |
4/6 = 2/3 |
| |
c |
1 time pay 20p
2 times pay 24p
60p
44p
16p |
| |
d |
16p / 6 = 22/3p |
| |
|
|
| 6 |
a |
12 |
| |
b |
1 |
| |
c |
23 |
| |
d |
1 |
| |
e |
4 |
| |
f |
1/4 |
| |
g |
5 |
| |
h |
£1.00 |
| |
i |
75p |
| |
j |
25p |
| |
|
|
| 7 |
|
| |
Red
die |
| 1 |
2 |
3 |
4 |
5 |
6 |
| Blue
die |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
| |
a |
4 |
| |
b |
36 |
| |
c |
4/36 = 1/9 |
| |
d |
6/36 = 1/6 |
| |
e |
1/36 |
| |
f |
6/36 = 1/6 |
Connections with Other Published Units from the Project
Other Units at the Same Level (Level 2)
Authors Anonymous
Opinion Matters
On the Ball
Getting it Right
Seeing is Believing
Units at Other Levels In the Same or Allied Areas of the Curriculum
Level 1
Shaking a Six
Probability Games
Leisure for Pleasure
Being Fair to Ernie
If at first ...
Level 2
Cutting it Fine
Level 4
Choice or Chance
Figuring the Future
Testing Testing
This unit is particularly relevant to: Mathematics.
Interconnections between Concepts and Techniques Used In these Units
These are detailed in the following table. The code numbers in
the left-hand column refer to the items spelled out in more
detail in Chapter 5 of Teaching Statistics 11-16.
An item mentioned under Statistical Prerequisites
needs to be covered before this unit is taught. Units which
introduce this idea or technique are listed alongside.
An item mentioned under Idea or Technique Used is not
specifically introduced or necessarily pointed out as such in the
unit. There may be one or more specific examples of a more
general concept. No previous experience is necessary with these
items before teaching the unit, but more practice can be obtained
before or afterwards by using the other units listed in the two
columns alongside.
An item mentioned under Idea or Technique Introduced
occurs specifically in the unit and, if a technique, there will
be a specific detailed instruction for carrying it out. Further
practice and reinforcement can be carried out by using the other
units listed alongside.
| Code No. |
Statistical
Prerequisites |
Introduced in |
| 4.1c |
Equally likely probabilities as expected
relative frequencies |
Shaking a Six
Probability Games |
| |
Ideas
and Techniques Used |
Introduced
in |
Also
Used in |
| 1.2a |
Using discrete data |
Seeing is Believing |
Shaking a Six
Probability Games
Leisure for Pleasure
Opinion Matters
Cutting it Fine
Being Fair to Ernie
If at first...
Authors Anonymous
Getting it Right
Figuring the Future |
| 1.3a |
Sampling from a small, well-defined
population |
|
If at first...
Authors Anonymous |
| 1.3c |
Sampling from distributions or infinite
populations |
|
Being Fair to Ernie
Cutting it Fine
If at first ... |
| 1.4a |
Data by direct counting |
Shaking a Six
Leisure for Pleasure
Getting it Right
Testing Testing |
Being Fair to Ernie
Cutting it Fine |
| 5i |
Estimating population figures from
samples |
Getting it Right |
On the Ball
Seeing is Believing |
| |
Ideas
and Techniques Introduced |
Also Used in |
| 1.3e |
Variability from samples |
Being Fair to Ernie
On the Ball
Choice or Chance
Probability Games
Getting it Right
If at first...
Cutting it Fine |
| 3.1c |
Mean for small data set |
If at first...
Seeing is Believing
Figuring the Future
Authors Anonymous
Getting it Right
On the Ball
Cutting it Fine |
| 3.1f |
Mean for frequency distribution |
Authors Anonymous
Seeing is Believing
Cutting it Fine |
| 4.1d |
Non-equally likely probability asthe
limit of relative frequency |
Probability Games
On the Ball
Testing Testing |
| 4.1m |
Fairness and equally likely
probabilities |
Probability Games
If at first...
Choice or Chance |
| 4.1 n |
Probability of a combination of events |
If at first... |
| 4.1o |
Systematic counting of outcomes |
Probability Games
Choice or Chance
Testing Testing |
| 4.3a |
Assumptions behind simple models |
|
| 5t |
Costs and risks in decision making |
|
| 5w |
Large samples better for inference |
Shaking a Six
Figuring the Future
On the Ball
Getting it Right |
| 5x |
Comparing actual with expected values |
Being Fair to Ernie
On the Ball
Testing Testing
Probability Games
Choice or Chance
If at first...
Figuring the Future |
Page R1
| |
Tally |
Number |
| Completely inside a square |
|
|
| Not inside a square |
|
|
| |
Total |
|
Table 4 - Penny pushing.
| Colour |
Prize value |
No. of fish |
Prize value x No. of
fish |
| Blue |
2p |
20 |
40p |
| Green |
3p |
10 |
|
| Yellow |
5p |
5 |
|
| Orange |
10p |
4 |
|
| Red |
25p |
1 |
|
Total Value
|
|
Table 5 - Prize fishing
| |
Spinner II |
 |
 |
 |
 |
 |
 |
| Spinner I |
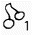 |
|
|
|
ca |
ca |
ca |
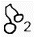 |
|
|
|
ca |
ca |
ca |
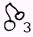 |
|
|
|
ca |
ca |
ca |
 |
|
|
|
|
|
|
 |
|
|
|
|
|
|
 |
|
|
|
|
|
|
Table 6 - Two-spinner fruit machine Spinner
II
|